3.2. Erste Berechnungen und Visualiserung#

In diesem Teil wird an zwei einfacheb mechanischem Beispielen eine Berechnung mit Python und die Möglichkeit der Visualiserung der erzeugten Daten aufgezeigt.

verwendete Bibliotheken:

  • numpy (Datenspeicherung und Berechnung)

  • matplotlib (Datenvisualisierung)

3.2.1. Beispiel 1: zweiseitig gelagerter Balken mit Linienlast#

Aufgabe: Berechnen Sie die maximale Durchbiegung

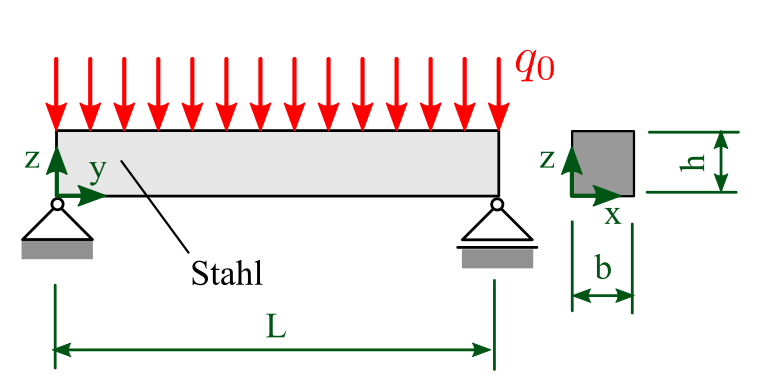
  • Länge: \(L = 1000\,\mathrm{mm}\)

  • Breite: \(b = 30\,\mathrm{mm}\)

  • Höhe: \(h = 30\,\mathrm{mm}\)

  • Linienlast: \(q_0=1000\,\mathrm{N}\)

  • E-Modul: \(E=200000\,\mathrm{MPa}\)

# Variablen
# Beispiel1: zweiseitig gelagerter Balken mit Linienlast
L = 1000.0 # mm
b = 30.0 # mm
h = 30.0 # mm
q = 1000.0 # N
E = 200000.0 # MPa -> N/mm^2

Berechnung des Flächenträgheitsmoments:

\[I=\frac{b\,h^3}{12}\]
# Lösung hier eintragen
I =

Berechnung der maximalen Durchbiegung

\[ u_{max}=\frac{5\,q\,L^3}{384\,E\,I} \]
# Lösung hier eintragen
umax =

3.2.2. Beispiel 2: einseitig eingespannter Balken mit Einzelkraft#

Aufgabe: Berechnen Sie die maximale Durchbiegung

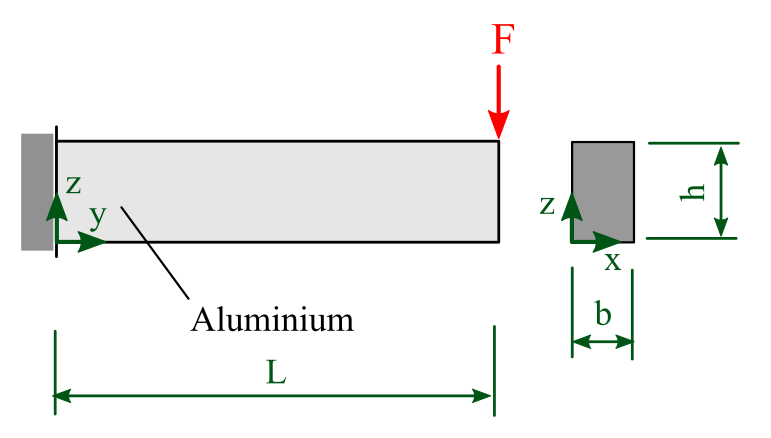
  • Länge: \(L = 1000\,\mathrm{mm}\)

  • Breite: \(b = 30\,\mathrm{mm}\)

  • Höhe: \(h = 60\,\mathrm{mm}\) Wert anders als im ersten Beispiel

  • Kraft: \(F=1000\,\mathrm{N}\) neuer Parameter

  • E-Modul: \(E=200000\,\mathrm{MPa}\) Wert anders als im ersten Beispiel

# Variablen
# Beispiel2: einseitig eingespannter Balken mit Einzelkraft
L = 1000.0 # mm
b = 30.0 # mm
h = 60.0 # mm
F = 1000.0 # N
E = 70000.0 # MPa -> N/mm^2

Berechnung des Flächenträgheitsmoments:

\[I=\frac{b\,h^3}{12}\]
I = (b*h**3)/12
print(I)

Berechnung der maximalen Durchbiegung

\[ u_{max}=\frac{F\,L^3}{3\,E\,I} \]
# Lösung hier eintragen
umax =

3.2.3. Darstellung der Durchbiegung in Abhängigkeit der Länge#

Aufgabe: Stellen Sie die maximale Durchbiegung in Abhängigkeit der Länge für beide Beispiele dar

3.2.3.1. Beispiel 1: zweiseitig gelagerter Balken mit Linienlast#

Wir wollen also statt einem Wert wie vorher gleich mehrere Werte berechnen. Dafür holen wir zunächst wieder die Parameter für das Beispiel:

Info: Wir speichern die Durchbiegung diesmal als Parameter umax1 ab, damit wir den Parameter für unser zweites Beispiel nicht überschreiben (da benutzen wir dann umax2) 
# Variablen
# Beispiel1: zweiseitig gelagerter Balken mit Linienlast
L = 1000.0 # mm
b = 30.0 # mm
h1 = 30.0 # mm
q0 = 1000.0 # N
E = 200000.0 # MPa -> N/mm^2
I = (b*h1**3)/12
umax1 = (5*q0*L**3)/(384*E*I)
print(umax1)

Nun erstellen wir für die Länge ein Array aus Werten mit Hilfe der numpy Bibliothek und dem Befehl np.array (Liste aus Werten)

import numpy as np
L = np.array([0,250,500,750,1000]) # mm
print(L)

Führen wir nun die Berechnung von oben erneut aus, wird durch die Verwendung einer Liste für den Parameter L, unser Ergebnis (also umax1) auch als Liste ausgegeben

umax1 = (5*q0*L**3)/(384*E*I)
print(umax1)

Zum plotten benutzen wir nun matplotlib und plotten mit plt.plot() und beschriften die Label mit plt.xlabel() und plt.ylabel()

import matplotlib.pyplot as plt
plt.plot(L,umax1);
plt.xlabel("Länge [mm]");
plt.ylabel("maximale Verschiebung [mm]");

Um die Werte zusätzlich als Punkte einzublenden kann:

plt.plot(marker="s",ms=10)

  • marker: “s” = square

  • ms = markersize (Größe der Punkte)

Übersicht über alle Stile (matplotlib Cheat Sheet)

plt.plot(L,umax1, marker="s",ms=10);
plt.xlabel("Länge [mm]");
plt.ylabel("maximale Verschiebung [mm]");

Um den Verlauf zu glätten sind mehr Punkte einzugeben, dafür ist np.linspace() sehr praktisch (in unserem Fall erstellen wir 20 Werte zwischen 0 und 1000)

L = np.linspace(0,1000,20) # mm
print(L)

Nun müssen wir umax1 erneut berechnen, da sich die Liste L ja geändert hat. Danach plotten wir erneut:

Info: Durch die Erhöhung der Anzahl der Datenpunkte es ist sinnvoll die marker (Befehl marker="s") wieder zu entfernen, da man sonst die Linie nicht mehr erkennt 
L = np.linspace(0,1000,20) # mm
umax1 = (5*q0*L**3)/(384*E*I)

plt.plot(L,umax1);
plt.xlabel("Länge [mm]");
plt.ylabel("maximale Verschiebung [mm]");

3.2.3.2. Beispiel 2: einseitig eingespannter Balken mit Einzelkraft#

Nun nehmen wir das zweite Beispiel und berechnen hier nun die Durchbiegung als umax2 damit wir später beide Parameter verwenden können und diese nicht überschrieben werden. Diesmal verwenden wir gleich np.linspace() für L um eine Liste von Werten für umax2 zu bekommen

# Variablen
# Beispiel2: einseitig eingespannter Balken mit Einzelkraft
L = np.linspace(0,1000,20) # mm
b = 30.0 # mm
h = 60.0 # mm
F = 1000.0 # N
E = 70000.0 # MPa -> N/mm^2
I = (b*h**3)/12
umax2=(F*L**3)/(3*E*I)
print(umax2)

Nun stellen wir dies erneut dar:

plt.plot(L,umax2);
plt.xlabel("Länge [mm]");
plt.ylabel("maximale Verschiebung [mm]");

3.2.3.3. Beide Beispiele zusammen#

Um beide zusammen darzustellen verwenden wir den Befehl plt.plot() einfach zweimal und benutzen den Parameter label= zur Bezeichnung und führen mit plt.legend() eine Legende ein

  1. Bezeichnung über label=

  2. Legende anzeigen mit plt.legend()

plt.plot(L,umax1,label="Beispiel 1");
plt.plot(L,umax2,label="Beispiel 2");
plt.legend();
plt.xlabel("Länge [mm]");
plt.ylabel("maximale Verschiebung [mm]");