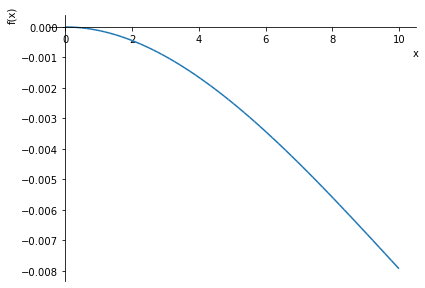
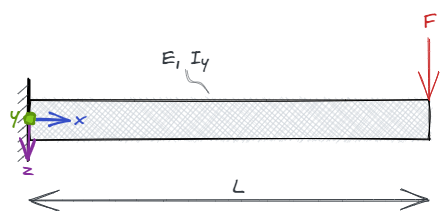
1. Eingespannter Balken mit Einzellast¶

Imports

from sympy import *
from sympy import init_printing
init_printing() 

Differentialgleichung definieren

E,Iy,x,L,F, M =symbols('E I_y x L F M')
u=symbols('u',cls=Function)
dglg=Eq(E*Iy*u(x).diff(x,2),-M)
dglg

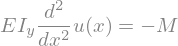
Momentenverlauf

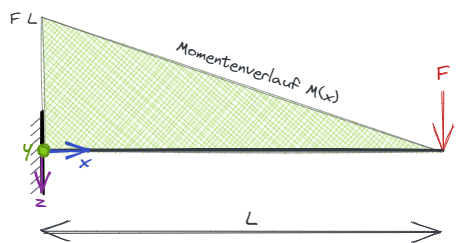
M=F*L+F*x

Falls nicht klar ist wie man auf die Gleichung kommt, hier eine mögliche Herleitung:

# y(x=0) = FL
x1=0
y1=F*L 

# y(x=L) = 0
x2=L
y2=0

M = (y2-y1)/(x2-x1) * (x-x1) + y1

Die komplette Differentialgleichung lautet dann wie folgt:

dglg=Eq(E*Iy*u(x).diff(x,2),-M)
dglg

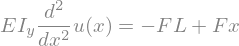
Differentialgleichung lösen

u=dsolve(dglg,u(x))
u

Integrationskonstanten mit Hilfe von Randbedingungen bestimmen

\(u(x=0) = 0\) -> muss umgestellt werden, so das Gleichung == 0 (ist bereits erfolgt)
\(u'(x=0) = 0\) -> muss umgestellt werden, so das Gleichung == 0 (ist bereits erfolgt)

Hinweis zum Umstellung der Gleichung ==0: Wäre die Randbedingung u(x=L)=1 so müsste stehen: u.rhs.subs(x,L)-1

bed1 = u.rhs.subs(x,0)
bed2 = u.rhs.diff(x).subs(x,0)
C = solve([bed1,bed2])
C

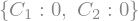
Integrationskonstanten einsetzen

u = u.subs(C)
u

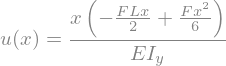
Gleichung vereinfachen

u.simplify()

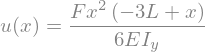
Daten einsetzen

Will man die das Ergebnis grafisch darstellen, so muss man Werte einsetzen

Beispieldaten:

Das Ergebnis ist dann in den Einheiten in denen die Beispieldaten gegeben sind (also hier in mm)

data=[(F,5),(L,10),(E,210e3),(Iy,1)]
ux = Lambda(x, u.rhs.subs(data))
ux

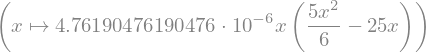
plotten

plot(ux(x),(x,0,L.subs(data)));