import pandas as pd
import numpy as np
from sympy import *
import math
from matplotlib import pyplot as plt
from sympy import init_printing
init_printing()
2. Normalkraftstab unter Eigenlast¶
2.1. Aufgabenstellung¶
Gegeben ist ein hängender Normalkraftstab mit zylindrischem Querschnitt unter Eigenlast.
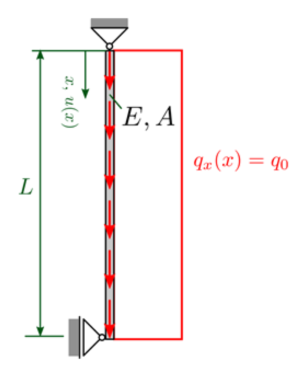
a) Zunächst verschaffen wir uns die exakte Lösung für das dargestellte Normalkraftproblem mit konstanter Dehnsteifigkeit und linear anwachsender Linienlast:
Lösen Sie die Differentialgleichung des Normalkraftstabes \((EA u(x)')'=-q_x(x)\) mit den Randbedingungen \(u(0)=0\) und \(u'(L)=0\).
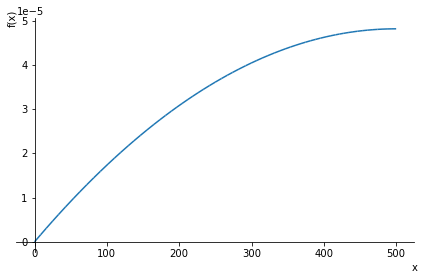
Stellen Sie den Verlauf von \(u(x)\) grafisch dar mit dem “Plot[]” Befehl.
Ermitteln Sie die Normalkraft \(N(x)\) (über \(N(x)= E A u'(x))\) sowie den Spannungsverlauf \(\sigma(x)\) und stellen den Verlauf üben den Stab dar.
b) Modellieren Sie das Problem in ANSYS und berechnen Sie ebenso den Verschiebungsverlauf \(u(x)\) und Spannungsverlauf \(\sigma(x)\). Vergleichen Sie die Maximalwerte und Verläufe mit den exakten Lösungen. Variieren Sie die Elementanzahl im Modell.
Geg.:
\(g=9,81\,\)m/s^2
\(\rho=7850\,\)kg/m^3
\(E=200.000\,\)GPa
\(A=2500\pi\)
\(L=500\,\)mm
Lösung a)¶
x,g,Em,rho,A,L =symbols('x g Em rho A L')
data=[(A,50**2*pi),(L,500),(rho,7.85*10**(-6)),(Em,200000),(g,9.81)]
u=symbols('u',cls=Function)
dglg=Eq(Em*A*u(x).diff(x,2),-A*g*rho)
dglg
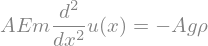
rb1=Eq(u(0),0)
rb1
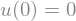
du=u(x).diff(x)
u=dsolve(dglg,u(x))
u

Die Konstanten können über die Randbedingungen mit solve bestimmt werden
bed1 = u.rhs.subs(x,0) - 0
bed2 = u.rhs.diff(x).subs(x,L) - 0
C = solve([bed1,bed2])
C
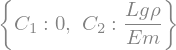
u = u.subs(C)
u
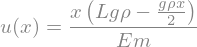
Die maximale Auslenkung ist dann
u.subs(data).subs(x,L.subs(data))
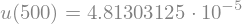
ux = Lambda(x, u.rhs.subs(data))
plot(ux(x),(x,0,L.subs(data)))
<sympy.plotting.plot.Plot at 0x217280b2f40>
Die Normalkraft errechnet sich aus der Ableitung der Verschiebungsfunktion
Nex=Lambda(x,Em*A*u.rhs.diff(x))
Nex
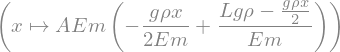
Die resultierende Kraft an der Lagerung ergibt sich zu
N(Nex(0).subs(data))

Damit ergibt sich die Spannung aus
Sigex=Lambda(x,Nex(x)/A)
Sigex(x)
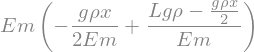
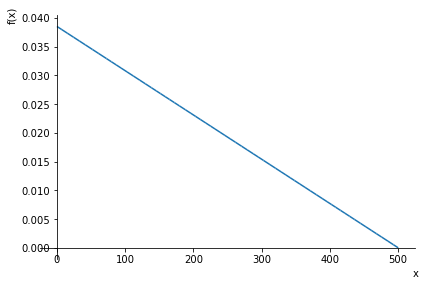
Und die grafische Darstellung des Spannungsverlaufes
plot(Sigex(x).subs(data),(x,0,L.subs(data)))
<sympy.plotting.plot.Plot at 0x21729846a60>
